Morevoer, since f'(x)0 in (infinity, 1) u (3,5), we see that f is decreasing in (infinity, 1) u (3,5) Example 2 Suppose f'(x) = (x1)(x3)(x7) , then f'(x)>0 in (infinity, 1) u (3,7) and hence f is increasing in those intervals On the other hand, f'(x)0 in (1,3) union (7, infinity), so f · Separate the intervals 0, π/2 to sub intervals in which f(x) = sin 4 x cos 4 x is increasing or decreasing(ii) lim x> x 0 f(x) exists (iii) f(x 0) = lim x > x 0 f(x) To know the points to be remembered in order to decide whether the function is continuous at particular point or not, you may look into the page " How to Check Continuity of a Function If Interval is not Given

Ex 6 2 4 Find Intervals F X 2x2 3x Is A Increasing
F(x) 0 over the intervals (–∞ –3) and
F(x) 0 over the intervals (–∞ –3) and-0 Department of PreUniversity Education, Karnataka PUC Karnataka Science Class 1219/5/18 · Show that the function F ( x)=∫ (from x to 3x)1/t dt is constant on the interval (0, ∞) Okay so I'm not sure if I should use the FTOC Part 1 or something else but this question is just really confusing It feels as though I'm forgetting the chain rule or something but I don't know how to implement it Even if I wanted to find F' (x) or



How Do You Determine Whether The Function F X Ln X 2 7 Is Concave Up Or Concave Down And Its Intervals Socratic
Transcribed image text 2 a Find the intervals on which f(x) = x cos x, 0 sxs it is increasing or decreasing b Prove that e* is an increasing function for x E R Prove that In x is an increasing function when x > 0 d It is given that f(x) = x x), for x > 0 Show that f is a decreasing function e It is given that f(x) = (2x 5)3 x, for x E R Show that f is a increasing functionGet an answer for 'Determine the intervals on which the function f(x)=x^x defined on the interval (0,∞) is decreasing and increasing' and find homework help for other Math questions at eNotes14/8/19 · Algebra 1 Graph the function and identify the domain and range y=5x^2 oo=infinite A) Domain (oo, oo) Range 0, oo) B) Domain (oo, oo) Range (oo, 0 C) Domain (oo, oo) Range (oo, 0 D) Domain (oo, oo) Range 0, oo) 2 How
Mathematical Consequences With the aid of the Mean Value Theorem we can now answer the questions we posed at the beginning of the section Consequence 1 If f0(x) = 0 at each point in an open interval (a;b), we can conclude that f(x) = C for some constant C for all x in the interval (a;b)DO For any $b$ in an interval as above, $f'(b)$ will never be 0, and $f'(b)$ will always be defined Why?6/7/18 · absolute maximum (5, 1/10) absolute minimum (0, 0) Given f(x) = x/(x^2 25) " on interval "0, 9 Absolute extrema can be found by evaluating the endpoints and finding any relative maximums or minimums and comparing their yvalues Evaluate end points f(0) = 0/25 = 0 => (0, 0) f(9) = 9/(9^2 25) = 9/(81 25) = 9/106 => (9, 9/106) ~~(9, 085) Find any relative
· Using the fact f ( x) > 0 on the interval where the graph is above the x axis, and f ( x) < 0 on the interval where the graph is below the x axis we have a f ( x) > 0 for x ∈ ( − 3, − 2) ∪ ( 0, 2) ∪ ( 3, ∞) b f ( x) < 0 for x ∈ ( − ∞, − 3) ∪ ( − 2, 0) ∪ ( 2, 3) Share answered Oct 14 '16 at 311That f(x) = 0 for some x in the interval (0;Example Find where $f(x) = x^3 3x^2$ is increasing/decreasing




Example 13 Find Intervals Where F X Sin X Cos X Is



Solved Unctions Cify The Associated Ranae Onramps Experience College Before College Hw 2 1 4 Function Increase And Decrease Definition If A Fun Course Hero
By the intermediate value theorem, there is some point x 0 with g(x 0) = 0, which is to say that f(x 0) − x 0 = 0, and so x 0 is a fixed point The open interval does not have the fixedpoint property The mapping f(x) = x 2 has no fixed point on the interval (0,1) The closed disc The closed interval is a special case of the closed discSo, suppose we need to find the Fourier series for the function f(x)=x defined on the interval (0,2) How can we do this since this function is not periodic?The function f(x) = 1 / x is continuous on interval (0, 1) but not uniformly continuous on It turns out that if we restrict ourselves to closed intervals both the concepts of continuity turn out to be equivalent Functions continuous on a closed interval are uniformly continuous on the same interval




Ppt Drill Determine The Intervals Of Increase And Decrease By Using The First Derivative Method Powerpoint Presentation Id




Question Video Finding The Intervals Where Functions Involving Logarithmic Functions Increase And Decrease Nagwa
Simple we make it periodic Consider one possible way of doing this The graph of our original function is 05 10 15 05 10 15 Fig 3 Graph of y = x on (0, 2)A) If f'(x) >0 on an interval, then f is increasing on that interval b) If f'(x) 0 on an interval, then f is concave upward on that interval d) If f''(x)Rolle's Theorem – Let f be continuous on the closed interval a, b and differentiable on the open interval (a, b) If f a f b '0 then there is at least one number c in (a, b) such that fc Examples Find the two xintercepts of the function f and show that f'(x) = 0 at some point between the two xintercepts 1 f x x x 3 2 f x x x31




4 4 Concavity And The Second Derivative Test Ppt Download
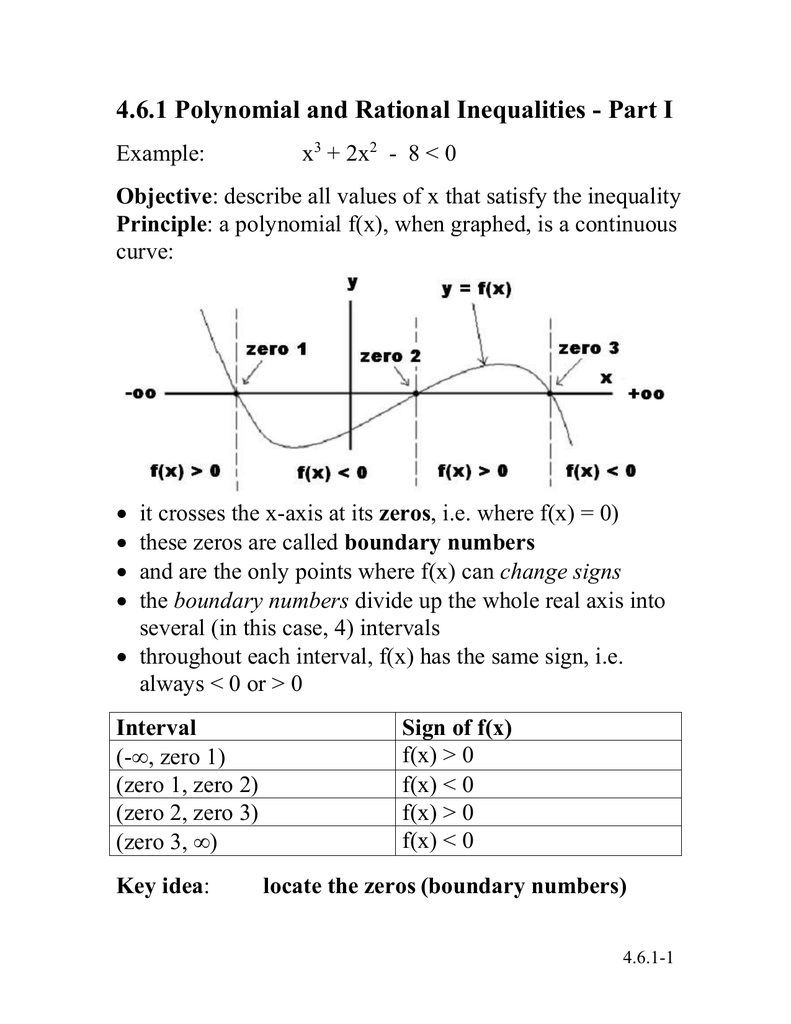



4 6 1 Polynomial And Rational Inequalities Part I
5/1/ · Determine the interval(s) for which f(x) ≥ 0 (Enter your answer using interval notation Enter EMPTY or ∅ for the empty set) f(x) = 8x 2 · Find the total area between \(f(x)=x−2\) and the xaxis over the interval \(0,6\) Solution Calculate the xintercept as \((2,0)\) (set \(y=0,\) solve for x) To find the total area, take the area below the xaxis over the subinterval \(0,2\) and add it to the area above the xaxis on the subinterval \(2,6\) (Figure)This suggests that we should try y=xd or y=xd If we go for the first, then we find c > 0 such that f is bounded on the interval (xd,xdc) Now let us try to be a bit more systematic We'll begin with x=0 and try to build up a larger and larger interval 0,t) on which f is bounded With luck, we'll be able to get t all the way up to 1
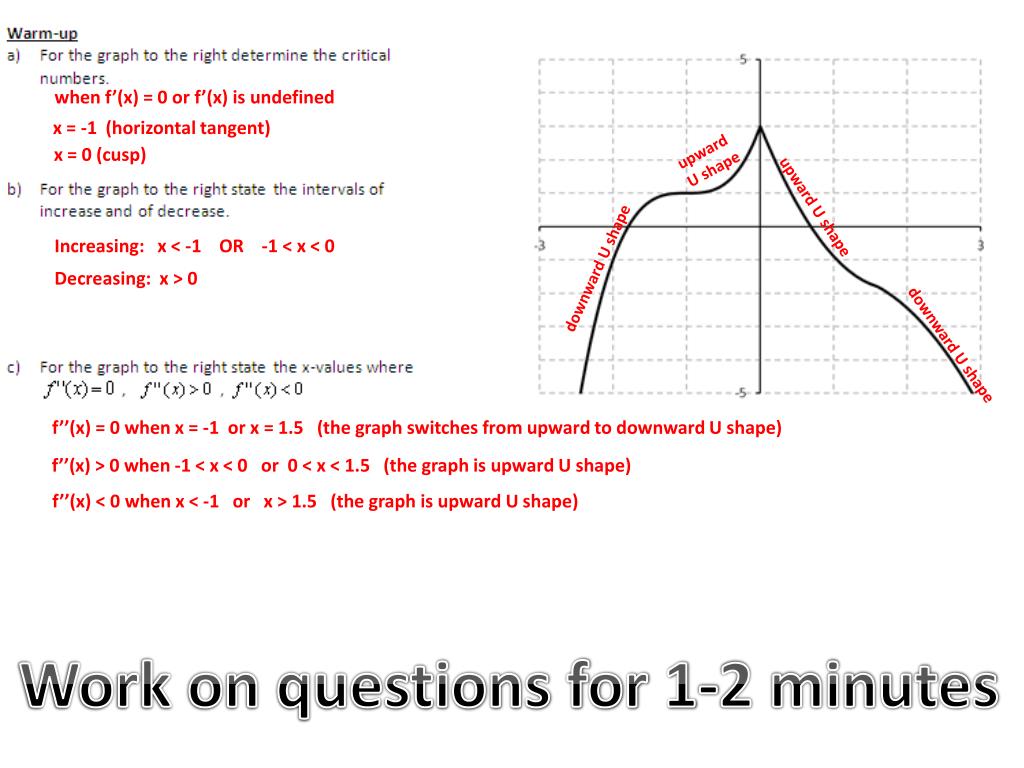



Ppt When F X 0 Or F X Is Undefined Powerpoint Presentation Id
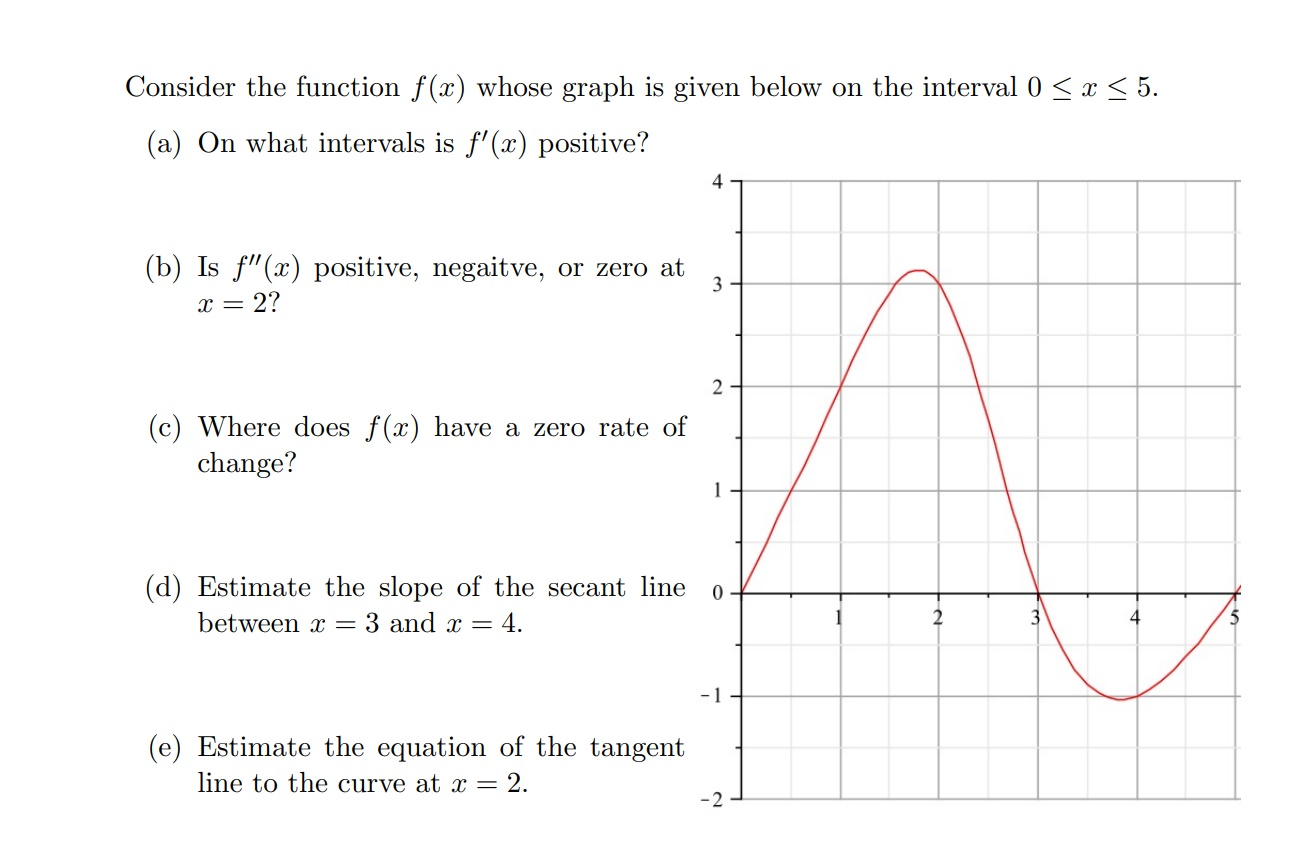



Consider The Function F X Whose Graph Is Given Below Chegg Com
3/2/ · If a, b ∈ R and a < b, the following is a representation of the open and closed intervals Open interval is indicated by (a, b) = {x a < y < b} Closed interval is indicated by a, b = {x a ≤ x ≤ b} The mandatory condition for continuity of the function f at point x = a considering a to be finite is that lim x→a– f (x) and limLet f be the function given by f(x)=x4(x−1)(x3) on the closed interval −5,5 On which of the following closed intervals is the function f guaranteed by the Extreme Value Theorem to have an absolute maximum and an absolute minimum?Answer to Consider the function f(x) = x^2 * sec(x) on the interval (0, pi) For which values of x does f(x) have a vertical asymptote?




Unit 3 Differentiation B C A Study
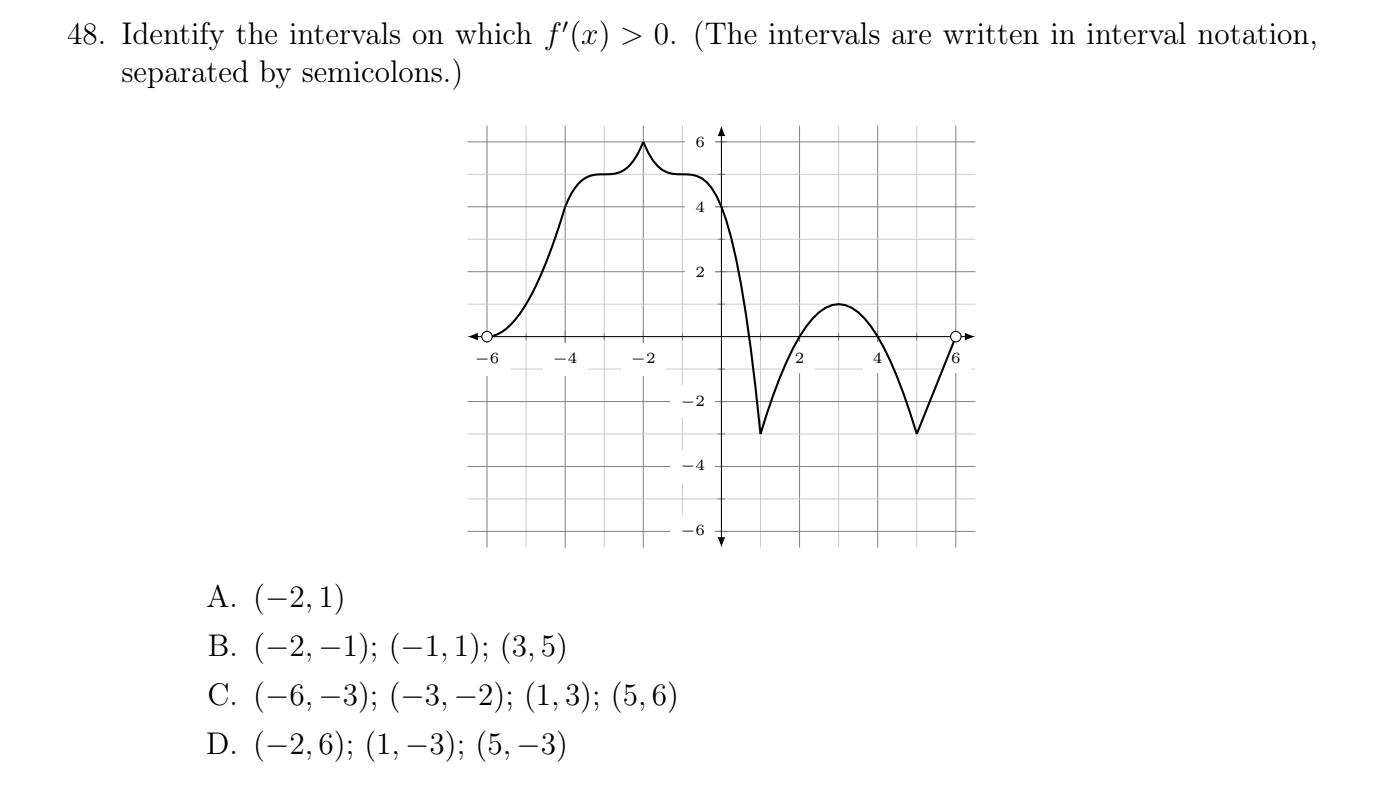



48 Identify The Intervals On Which F X 0 The Chegg Com
Consider the function on the interval (0, 2𝜋) f(x) = 5 sin2(x) 5 sin(x) (a) Find the open interval(s) on which the function is increasing or decreasing (Enter your answers using interval notation)X = 4 Thus, the1) Find the interval(s) on which f(x)>0 and f(x)0 and Find the interval(s) on which f(x)0 and f(x)0 and f(x)




Which Statement Is True About The Given Function A F X 0 Over The Intervals Infinity 2 7 And 0 8 Infinity B F X 0 Over The Intervals Infinity 2 7 And 1 0 8




Find Intervals In Which The Function Given By F X Sin3x X 0 Pi 2 Is A Increasing B Decreasing
X 1 (a) 2,2 (b) 1,1 (c) 2, 1 (d) ( 0, 1 (e) 1,2Let us return to the Riemann sum Consider, for example, the function f(x) = 2 − 2x2 (shown in Figure 117) on the interval 0, 2 Use n = 8 and choose {x * i } as the left endpoint of each interval Construct a rectangle on each subinterval of height f(x * i) and width Δ xSolution for On what interval is the function f (x) = increasing?




Which Statement Is True About The Graphed Function F X Lt 0 Over The Intervals 0 7 And Brainly Com




Ethiopia Learning Math Grade 12 Page 492 In English
(a) If f0(x) > 0onaninterval,thenf is increasing on that interval (b) If f0(x) < 0onaninterval,thenf is decreasing on that interval Example 1 Find the intervals on which f(x)= 1 4 x4 2 3 x3 is increasing and decreasing The First Derivative Test Suppose that c is a critical number of a continuous function f14/4/21 · Transcript Ex 62, 6 Find the intervals in which the following functions are strictly increasing or decreasing (a) 𝑥2 2𝑥 – 5 f(𝑥) = 𝑥2 2𝑥 – 5 Calculating f' (𝒙) f'(𝑥) = 2𝑥 2 f'(𝑥) = 2 (𝑥 1) Putting f' (𝒙) = 0 2 (𝑥 1) = 0 (𝑥 1) = 0 𝒙 = –1 Plotting point on real line Hence, f is strictly decreasing for (−∞ ," –1" ) f isClick here👆to get an answer to your question ️ Find the intervals in which f(x) = (x 2)e^x is increasing or decreasing




Please Solve Example Find The Intervals In Which Fx Sin3x Cos3x 0 X P Is Strictly Increasing Or Decreasing Maths Application Of Derivatives Meritnation Com




Rd Sharma Solutions For Class 12 Maths Chapter 17 Increasing And Decreasing Functions Download Free Pdf
19/4/21 · Ex 63 → FacebookWhatsapp Transcript Ex 62, 3 Find the intervals in which the function f given by f (𝑥) = sin 𝑥 is (a) strictly increasing in (0 , 𝜋/2) f(𝑥) = sin 𝑥 f'(𝒙) = cos 𝒙Since cos 𝑥 > 0 for 𝑥 ∈ ("0 , " 𝜋/2)∴ f'(𝑥) < 0 for 𝑥 ∈ (0 , π) Thus, f is strictly increasing in ("0 , " 𝜋/2)Roughcos 0 = 1Increasing/Decreasing Test If f′(x) > 0 for all x ∈(a,b), then f is increasing on (a,b) If f′(x) < 0 for all x ∈(a,b), then f is decreasing on (a,b) First derivative test Suppose c is a critical number of a continuous function f, then Defn f is concave down if the graph of fI Then f(I) is an interval 02 Uniform Continuity First recall the de nition of fbeing continuous at x 0 8 >09 >0 38x jx x 0j< =)jf(x) f(x 0)j< In general, depends on both and x 0, as function changes rapidly at some points and at at some other points We start some examples to look into this Example 021 Let f R !R and f(x) = 2x Let
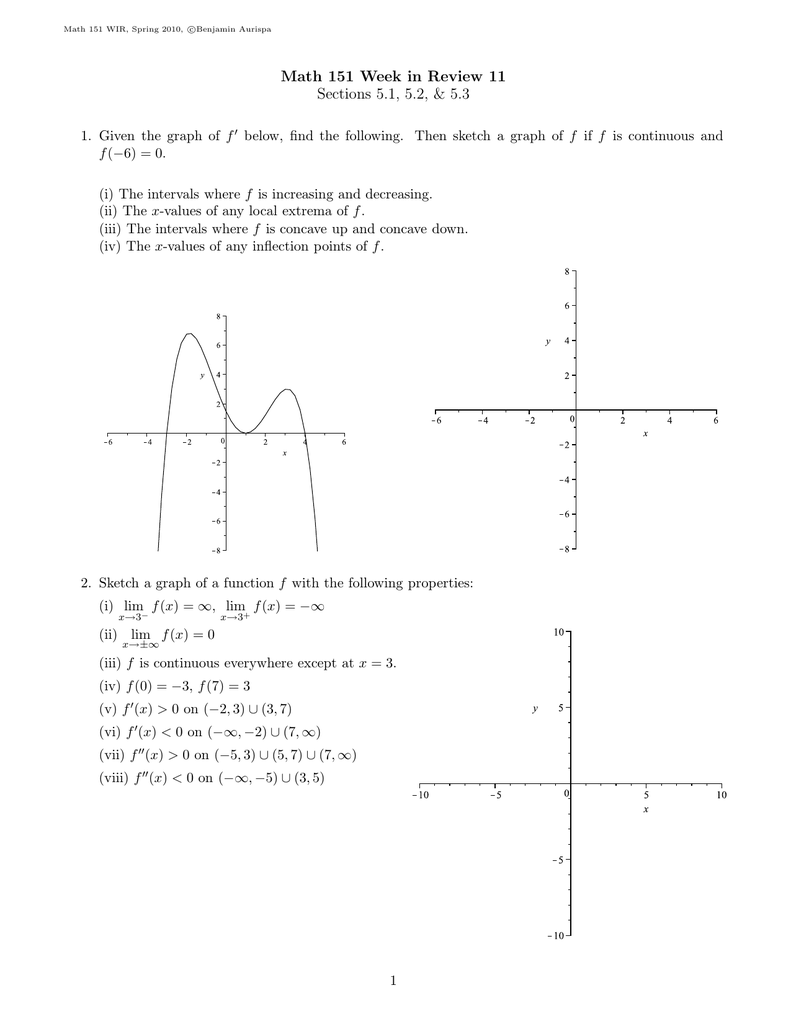



Document



Solved Let F X X Lnx 2 For X Gt 0 Find The Intervals On Which F Is Increasing Or Decreasing Nd The Local Maximum And Minimum Values Of F Course Hero
· 33 1 A graph of a function f used to illustrate the concepts of increasing and decreasing Even though we have not defined these terms mathematically, one likely answered that f is increasing when x > 1 and decreasing whenIncreasing/Decreasing Test If f ′ (x) > 0 on an open interval, then f is increasing on the interval If f ′ (x) < 0 on an open interval, then f is decreasing on the interval DO Ponder the graphs in the box above until you are confident of why the two conditions listed are trueTo determine the critical points, set f′(x) = 0 f ′ ( x) = 0 −3x212x = 0 −3x(x−4) = 0 ∴x = 0;




Reading The Graph Of A Function Intervals On Which Fx Is Positive Negative Youtube




Find The Intervals In Which F X 4x 2 1 X Is Increasing Or Dec
(i) f(x) must be defined in a neighbourhood of x 0 (ie, f(x 0) exists);This is because $f'(x)$ is positive at $x=b$, and can't change sign anywhere else in the interval (similarly if $f'(b)$ is negative) Remember $f'(x)$ can only change sign at critical points!To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Find the intervals in which the function `f` given by f(x) = sin x cos x, 0 `




Ex 6 2 4 Find Intervals F X 2x2 3x Is A Increasing



Ap Calculus Ab Multiple Choice 1998 Exam Part B Videos Questions Solutions
Separate the intervals Choose random value from the interval and check them in the first derivative If f (x) > 0, then the function is increasing in that particular interval If f (x) < 0, then the function is decreasing in that particular interval3/2/19 · If f(x) = x/2 1, then on the interval 0, pi (a) tan f (x) and 1/f(x) are both continuous (b) tan f (x) and 1/f(x) are both discontinuous (c) tan f (x) and f1 (x) are both continuous (d) tan f (x) is continuous but 1/f(x) is not continuous16/7/17 · The left riemann sum requires you to use the lower number in every interval listed above as your x term, and then evaluate the functional value at that particular x value, like this Note that 2 would be the width of every rectangle formed, since the intervals are of equal width 1Area1 = f (0) ⋅ 2 = 02 ⋅ 2 = 0




4 Solved Problems On The Polynomial Functions Study Guide Math 180 Docsity




Find The Intervals In Which The Function F X 2x 3 15x 2 36
For our second interval (1,1), let the test value be x=0 `f'(0)=(10^2)/(0^21)^2=1` (Increasing) And for our third interval, let the test value be x=21) (this gets some marks) Because f is a ff of a polynomial and an exponential function, it is continuous everywhere, in particular, on the closed interval 0 ;On which of the following intervals is the function f (x) = 2x^2 log x, x≠ 0 increasing in 12th Maths Application of Derivatives Increasing and Decreasing Functions On which of




Find The Intervals In Which Function F X Sin X Cos X 0 Lt X L



How Do You Determine Whether The Function F X Ln X 2 7 Is Concave Up Or Concave Down And Its Intervals Socratic
12/2/19 · The maximum on the interval could be a local maximum somewhere within the interval, or it could be a value at one end or the other You can calculate all three and compare them To get started a sketch may help you get a sense of what the curve looks likeFind the Intervals in Which F(X) = Sin X − Cos X, Where 0 < X < 2π is Increasing Or Decreasing ?Algebra Convert to Interval Notation x>=0 x ≥ 0 x ≥ 0 Convert the inequality to interval notation 0,∞) 0, ∞)




5 1 Derivatives And Graphs Pdf Free Download




Interval Of F X Question Find The Intervals On Which F X 3x 4 4x 3 12x 2 2 Is My Working Out And Answer Correct Askmath
On 0 < x < 4, f′(x) > 0 so f(x) is increasing On x < 0, and on x > 4, f′(x) < 0 so f(x) is decreasing (c) Find the inflection points of f(x) f′′(x) = 12x2e−x −4x3e−x − 4x3e−x x4e−x = x2e−x(2− x)(6− x) Inflection points x = 2,6 (d) Find the intervals of concavity On x < 2, and on x > 6, f′′(x) > 0 so f(xX= 4 − 3 x 2 12 x = 0 − 3 x ( x − 4) = 0 ∴ x = 0;Which contradicts that f0(x) 6= 1 on the interval containing d,e Exercise 537(a) Let f (a,b) → R be an increasing function that is also differentiable on (a,b) If c ∈ (a,b) then f0(c) = lim x→c f(x)−f(c) x−c Let x n → c with x n > c, then we have that f(x n) − f(c) ≥ 0 since the function is increasing and x n − c




Question 5 Select All Intervals On Which The Funct Gauthmath



Answered Use The Given Graph Of Y F X To Find Bartleby
Conversely, if \(f'(x) > 0\) for every \(x\) in the interval, then the function \(f\) must be increasing on the interval Notice that we have to have the derivative strictly positive to conclude that the function is increasing1 (this gets some marks)Solution for Find the intervals where f"(x) < 0 or f"(x) > 0 as indicated f"(x) < 0 (1, 0) O (1, 0) (00, 1) (1, 0), (1, o0)




Mtl107 Set 1 Discrete Mathematics Real Analysis
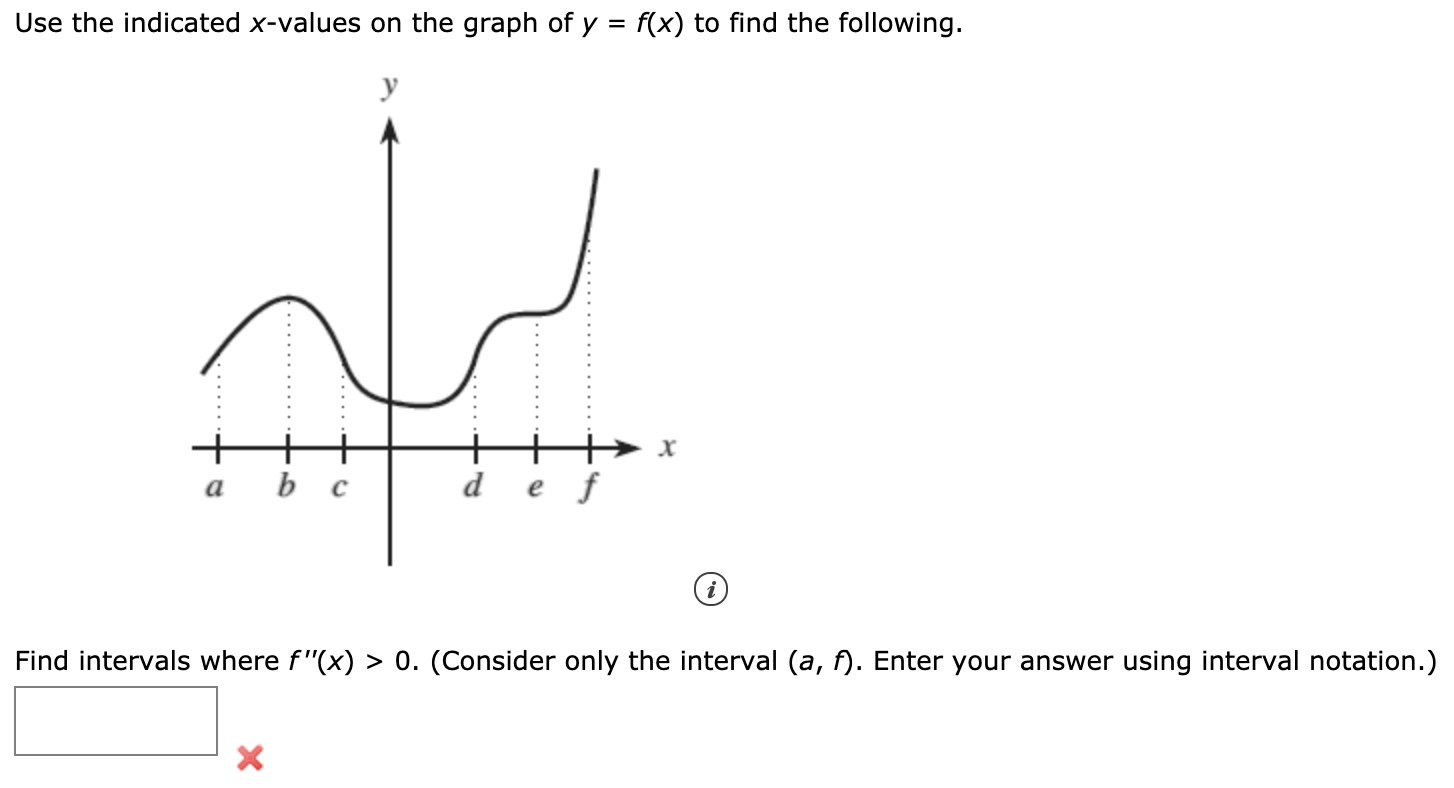



Solved Use The Indicated X Values On The Graph Of Y F X Chegg Com




Solutions Manual For Calculus And Its Applications 11th Edition By Bittinger Ibsn By Corbin000 Issuu



Studying The Intervals Of Increase And Decrease Of Functions 1 Video Dailymotion




Question Video Finding The Intervals Of Increasing And Decreasing Of A Rational Function Nagwa




Misc 7 Find Intervals F X X3 1 X3 X 0 Is Increasing




Increasing And Decreasing Functions Ppt Download




Question Video Finding Intervals Where A Polynomial Function Increases And Decreases Nagwa




Use The Given Graph Of F Over The Interval 0 7 To Find The Following A The Open Intervals On Which F Is Increasing Enter Your Answer Using Interval Notation B The Open




Mathematics Notes
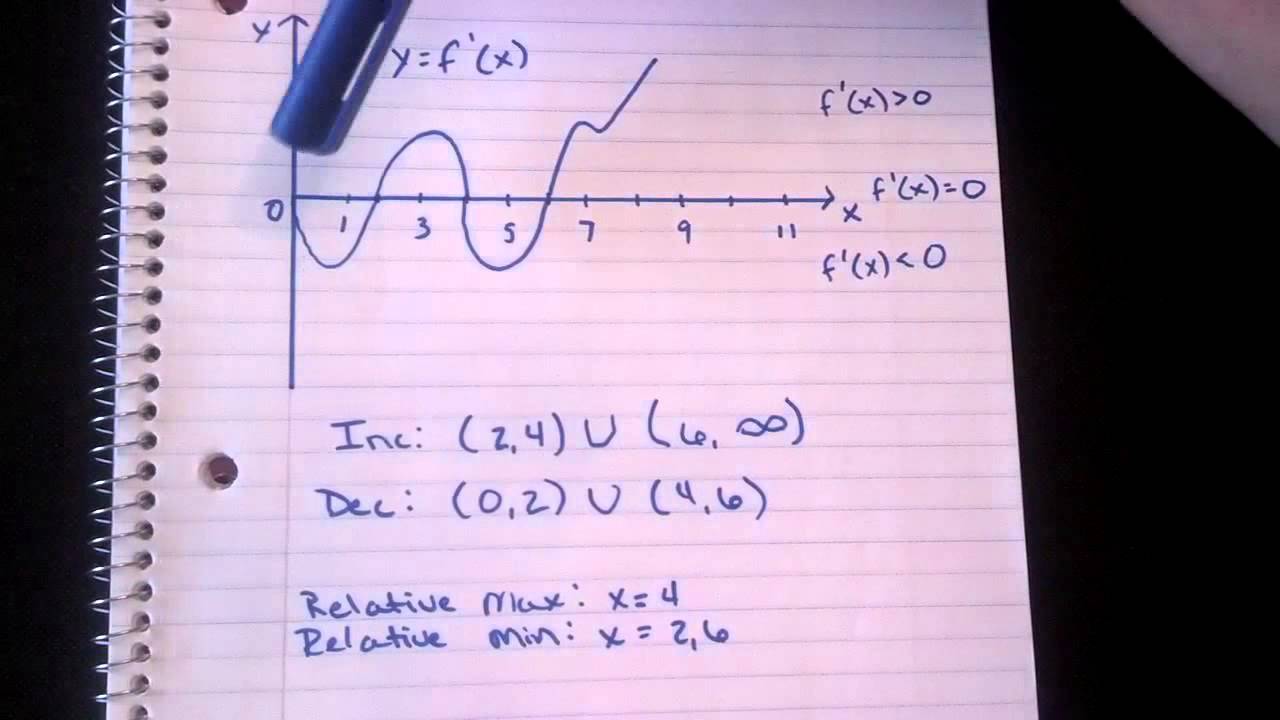



How To Use The Graph Of F To Identify The Intervals On Which F Is Increasing Or Decreasing Youtube



4 3 Webassign Answers




First Year Calculus Chapter 7 Continuity It Is A Parabola And We Can Draw This Parabola Without Lifting Our Pencil From The Paper Pdf Free Download




Solved Use The Graph Of Y F X Assuming F X 0 If X Chegg Com




Project 7 Studocu




Use A Graph To Determine Where A Function Is Increasing Decreasing Or Constant College Algebra




Find The Intervals In Which The Function F Given By F X Sinx Cosx 0 X 2pi Is Strictly Increasing Or Strictly Decreasing




Increasing Decreasing Functions Ocr As Maths Pure Revision Notes




Increasing Decreasing Positive Or Negative Intervals Video Khan Academy




Zqeyr9lussxoxm




Ap Calculus Ab Calculus Tracy Unified School District Calculus Ap Ap Fr Ap Calculus Pdf Document




Solved Question 6 25 Assignment Given Function F X Real Interval B Numerical Integration F X Inte Q




Finding Decreasing Interval Given The Function Video Khan Academy
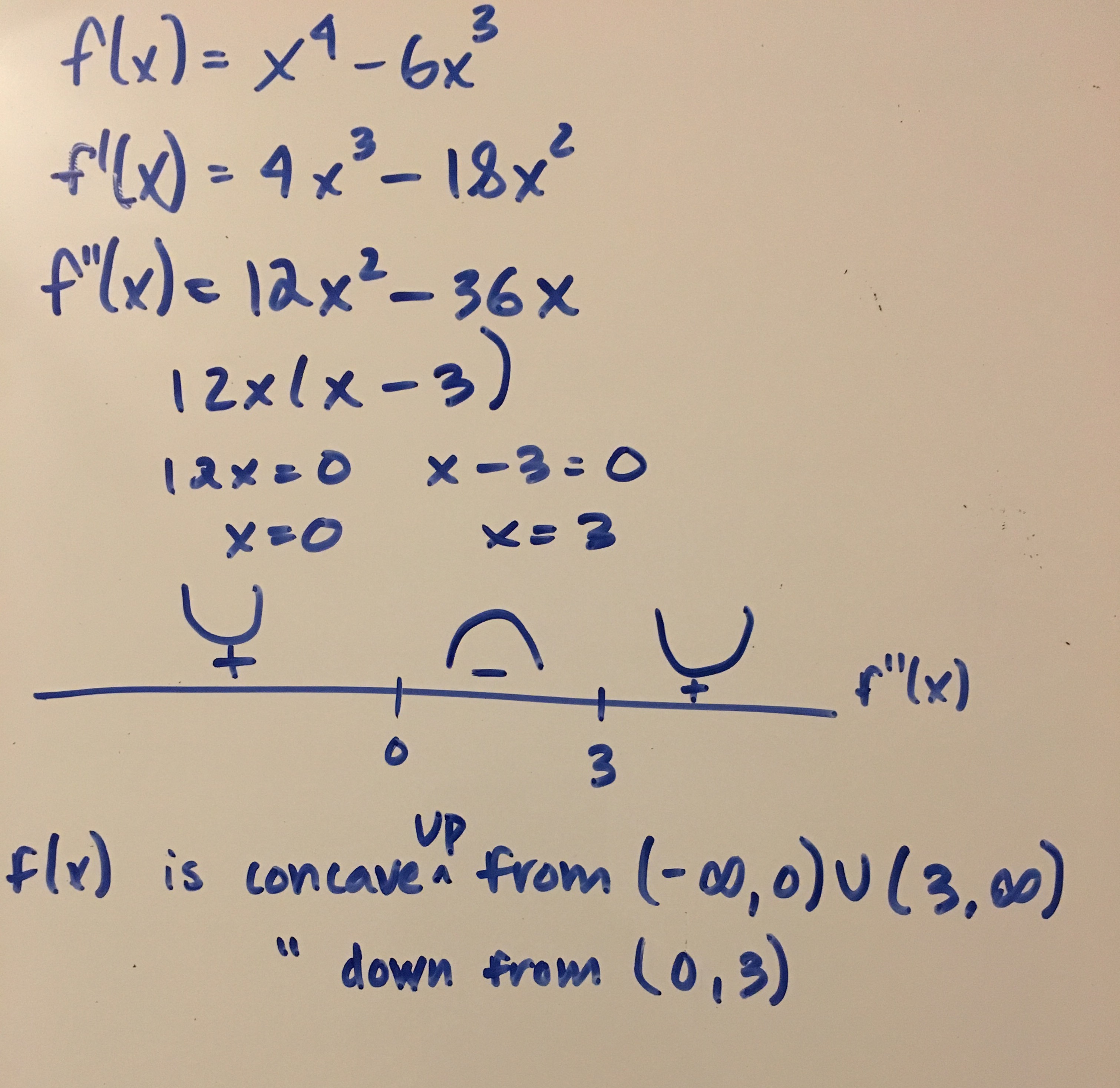



How Do You Ise Interval Notation Indicate Where F X Is Concave Up And Concave Down For F X X 4 6x 3 Socratic




F X Frac X 4 4 Frac X 3 3 X 2 Find The Intervals On Which F Is Increasing And Decreasing And Identify The Local Extrema Of F Mathematics Stack Exchange




Select The Interval Where F X Gt 0 Brainly Com
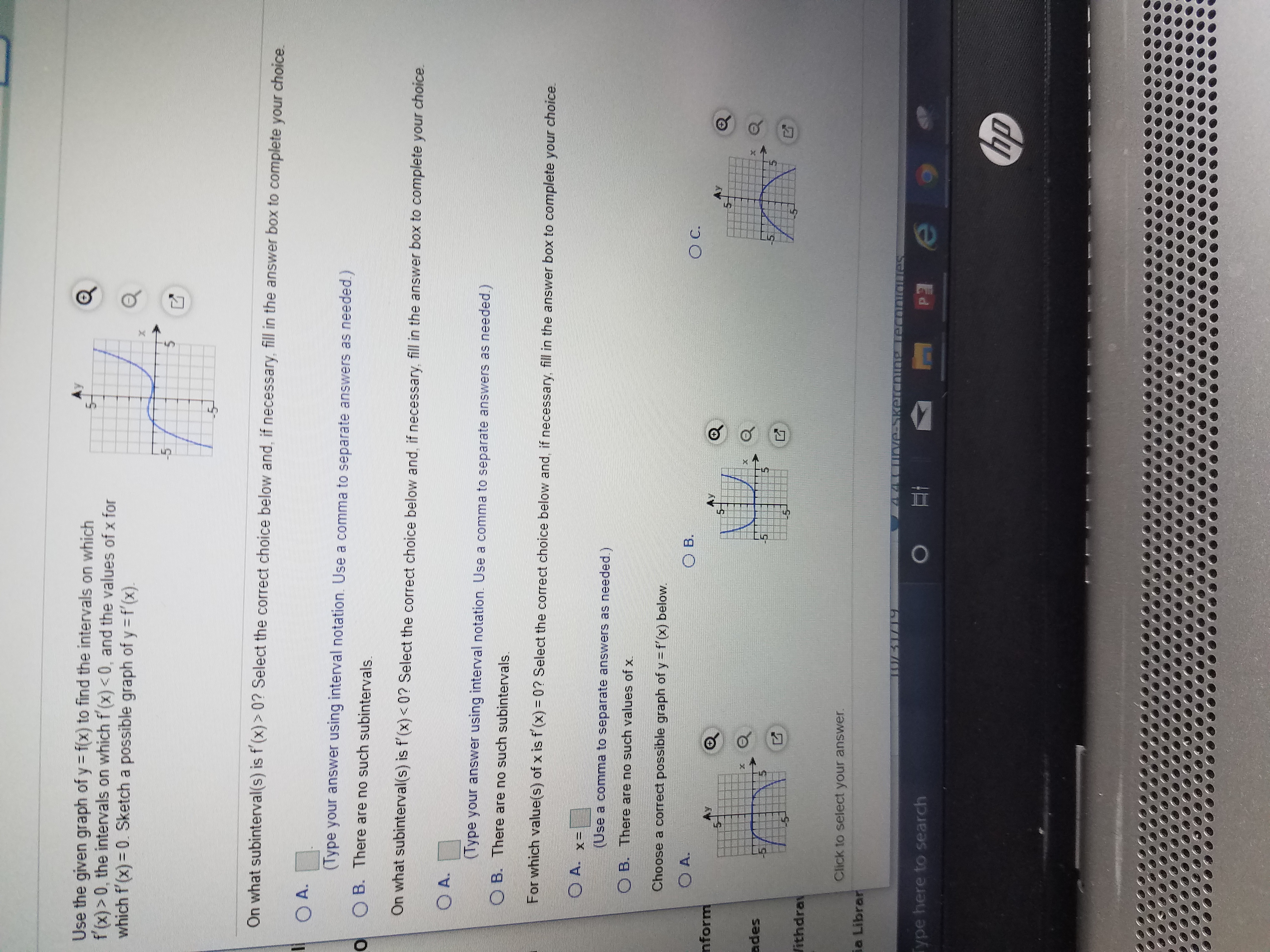



Answered Use The Given Graph Of Y F X To Find Bartleby
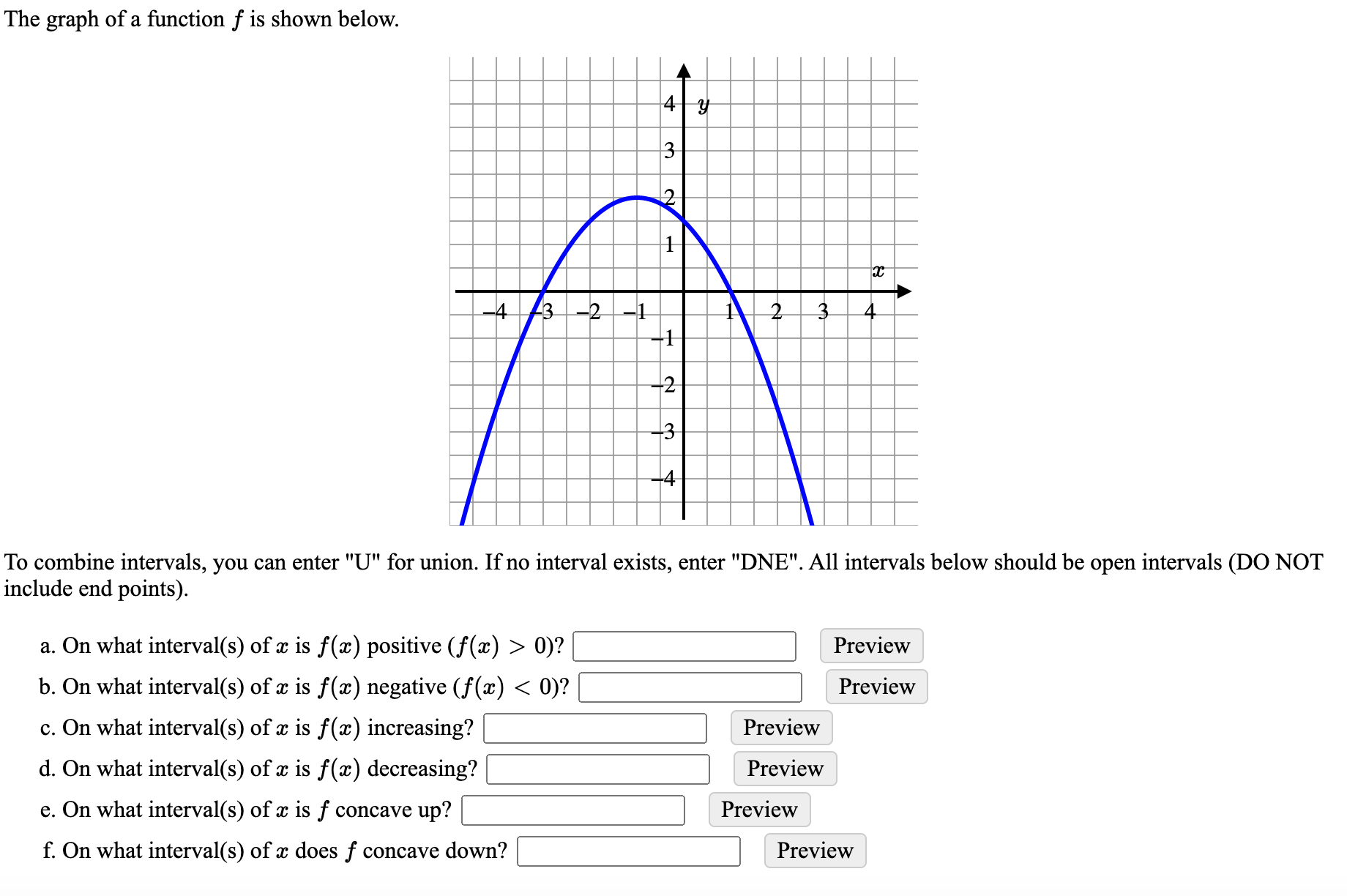



Answered The Graph Of A Function F Is Shown Bartleby




Pdf Initial Boundary Value Problems For Nonlinear Dispersive Equations Of Higher Orders Posed On Bounded Intervals With General Boundary Conditions




Ex 2 Intervals For Which The First And Second Derivative Are Positive And Negative Given A Graph Youtube



0 件のコメント:
コメントを投稿